网络信息安全|第1章:密码学基础 - 加密与解密
Synopsis: 本文介绍了对称加密、公钥加密、单向加密的作用,比如公钥加密主要用于密钥交换和身份验证,对称加密用于会话数据的加密,单向加密的主要用途是验证消息和文件的完整性,我们只研究算法的用途,至于像 RSA、DH 算法的实现原理那是数学家的事。然后详细说明如何实现身份认证和密钥交换,并为了解决公钥的安全传输问题引入了数字证书和CA,最后用流程图解释了如何进行安全的加密和解密。要想理解下一篇文章 SSL/TLS 的原理,必须先完全理解本文的理论知识
1. 信息安全
1.1 CIA 原则
数据保密性(confidentiality): 确保数据传输时不会被未授权的第三方窃听,需要进行加密(encrypt),防止数据泄密数据完整性(integrity): 确保数据传输时不会被非法篡改或损坏,保证数据的一致性数据可用性(availability): 保证已授权的用户对数据的使用不会被不正当地拒绝,常使用冗余、故障转移、RAID、高可用集群等技术进行保障
1.2 加密与解密
加密、解密及破译的技术统称 密码学,密码学的基本原则:算法要公开、密钥要随机
将 明文(plaintext) 通过加密算法和密钥转换成难以阅读的 密文(ciphertext) 的过程,叫做 加密(encrypt)。相反,将密文转换成明文的过程叫做 解密(decrypt)

如果直接传输明文(比如 HTTP 协议),则数据在网络传输的过程中,所经过的每一个路由节点时,都可能被查看,黑客可以很简单地就能截获你的登录用户名和密码:

如果对数据进行加密后,传输密文(比如 HTTPS 协议),则黑客截获到密文也无济于事:
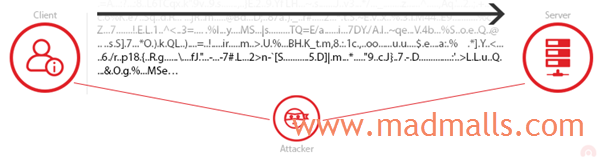
Ciphersare methods/algorithms used to encrypt and decrypt data
2. 对称加密
对称加密(symmetric encryption) 又称为 私钥加密(private-key cryptography),它在 加密(encrypt) 和 解密(decrypt) 的过程中使用 相同的密钥。1976 年以前,所有的加密方式都是对称加密,如何安全地的保管和传递密钥,成了最头疼的问题
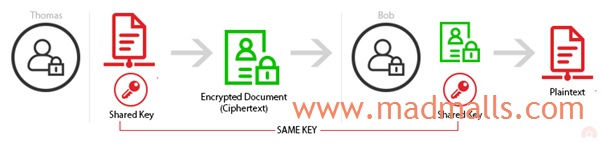
对称加密 可分为 分组密码(block ciphers) 和 流密码(stream ciphers) 两类算法
2.1 Block Ciphers
Block Ciphers 将明文分隔成固定大小的块(比如 64-bit 或 128-bit),逐个进行加密,加密速度快。但是也有问题,如果最后一块数据不足时,需要添加 padding(通常使用随机数据来填充块),目前已发现很多针对分组密码使用的填充的 漏洞。流行的 Block Ciphers 包括:DES、3DES、AES、Blowfish 和 RC5 等
Initialization Vector (IV)
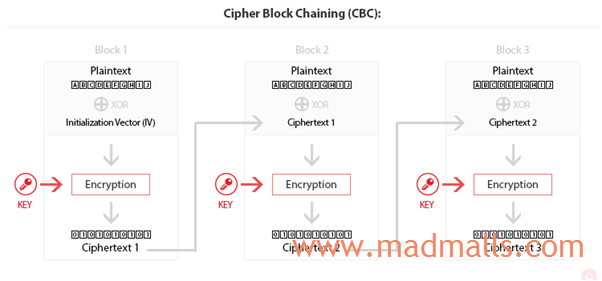
Initialization Vector (IV) 用于启动分组密码,它是固定大小的随机或伪随机(pseudo-random)输入。比如下文的 Cipher Block Chaining (CBC) 模式中,每个块要与前一个块进行 异或(XOR),但第一个块没有前序块能进行异或,所以 IV 就用于第一个块的输入用以启动加密。因为 IV 通常使用随机数,那么每次加密时它都不一样,所以它还用于防止攻击者通过猜测 IV 来解密所有消息。另外,如果它使用随机数,则使用相同的对称密钥加密相同的明文,其输出将是不同的密文
2.2 Stream Ciphers
Stream Ciphers 以任意长度的 伪随机(pseudo-random)序列(也称为 key streams)来加密数据流。流密码是一种流行的选择,因为它们易于实现且速度快。实际上,关于上述分组密码问题的最佳解决方法是将分组密码设置为流密码,这称为 counter mode,最常见的示例就是下方的 Cipher Block Chaining (CBC) 模式(CBC 已经不安全,TLS v1.3 中不能再使用)。流行的 Stream Ciphers 包括:RC4、CHACHA20 等(RC4 已经不再安全)
2.3 Block Cipher Operation Modes
分组密码 模式 是为了加密任意长度的数据而设计的密码学方案,是对分组密码的扩展。注意,有些模式会将分组密码转换成流密码。所有分组密码模式都支持数据机密性,不过有些还同时支持消息认证,比如 AES-128-CCM 和 AES-GCM 系列都支持 AEAD(见章节 4.3)
(1) Electronic Code Book (ECB)
使用 ECB 时,每个数据块都是单独加密的,然后按原始顺序连接起来。由于块不相互依赖,因此可以进行并行处理。而且不需要 IV。ECB 的主要问题是如果相同的数据块被加密,它将始终生成相同的密文,这使得攻击者很容易根据重复模式来猜测出原始数据

(2) Cipher Block Chaining (CBC)
使用 CBC 时,每个块在加密前与先前的密文进行异或,这样即使是相同的数据块也会生成不同的密文。需要 IV 来加密第一个明文块。由于块是链接的,因此不可能进行并行处理。CBC 有一个主要缺点:如果消息的一部分出现乱码或丢失,则消息的其余部分将丢失
(3) Cipher Feedback (CFB)
CFB 方法将块密码转换为自同步流密码,这意味着如果消息的一部分是乱码或丢失,则密码可以在几个块之后同步,并且消息的其余部分不一定丢失
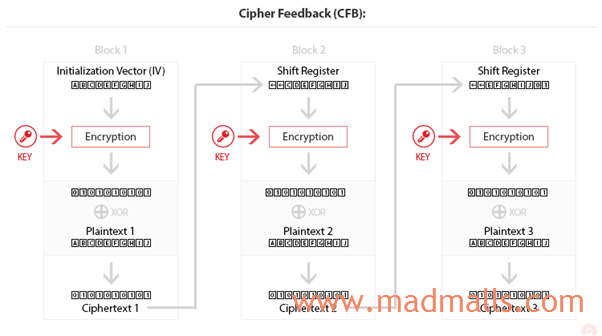
(4) Output Feedback (OFB)
OFB 方法创建同步流密码,该技术保留了纠错码(error correction codes),加密和解密过程完全相同
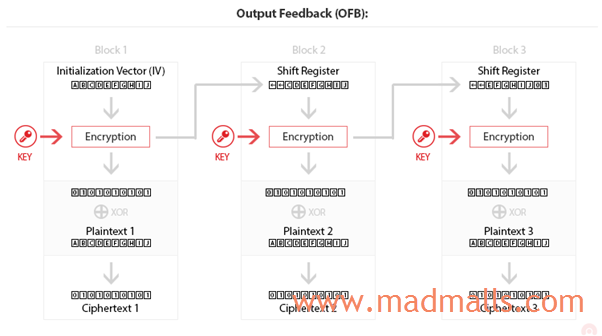
(5) Counter Mode (CTR)
CTR 方法类似于 OFB,因为它还创建了一个同步流密码。但是,它为每个块使用 counter 和nonce(在加密通信中仅使用一次的密钥,这个值必须唯一),并且不将块链接在一起。因此,可以并行加密和解密块
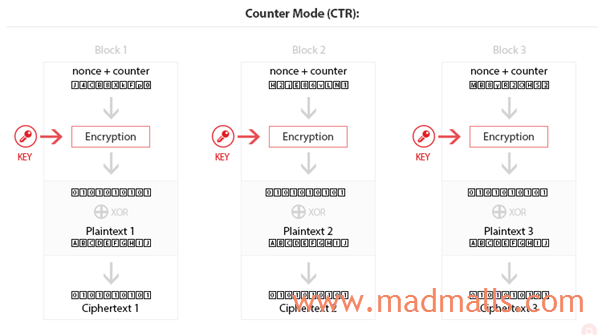
(6) Counter mode with CBC-MAC (CCM)
CCM 是一种提供经过身份验证的(MAC)、加密的分组密码模式,此模式仅针对块长度为 128-bit 的块密码(比如 AES-128-CCM)。另外,由于 CCM 是 CTR 的推导(它实际上是一个流密码),所以要仔细选择 CCM 的 nonce,防止某指定的 密钥 会被多次使用(不安全)
(7) Galois/Counter Mode (GCM)
建议使用支持 AEAD 的更安全、高效的 AES-GCM 系列算法,详情见本文章节 4.3
3. 非对称加密
对称加密 可以快速加密大量的数据,但双方如何安全的传输密钥,而不被第三方窃取呢?1976 年,美国密码学家 Whitfield Diffie 和 Martin Hellman 发表了 Diffie–Hellman key exchange,可以通过不安全的公共信道交换 DH 参数,就能创建出只有双方知道的 共享秘密(shared secret),实现原理见本文的章节 6.2 的描述
Diffie–Hellman 密钥交换 算法是现代密码学的里程碑,开创了 公开密钥密码学。1977 年,三位数学家 Ron Rivest, Adi Shamir 和 Leonard Adleman 受 DH 算法的启发,发明了 RSA 算法(以姓的首字母命名)
非对称加密(asymmetric encryption) 又称为 公钥加密(public-key cryptography),因为它使用一对密钥,包含一个 私钥(Private Key/Security Key) 和一个 公钥(Public Key)。私钥不公开,由拥有者小心地保管。公钥是从私钥中提取产生,可公开给所有人(如果使用对称加密,你想从 100 个人那安全地接收消息,你就需要维护 100 个不同的密钥并发给各自的人。而使用公钥加密,你只需要一对密钥,并将公钥发给其它人,这样任何人都可以向你发送消息,且只有你可以阅读)
如果用 公钥 加密数据,就必须用配对的 私钥 才能解密,反之亦然
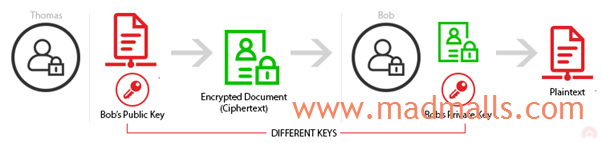
于是,任何人都可以使用接收者 Bob 所公开的 公钥 来加密数据,且只有接收者 Bob 才能用自己的 私钥 解密
但是,公钥加密 很少被用来加密大量的数据,因为它的速度很慢,比 对称加密 差不多慢 10,000 倍。公钥加密的密钥越长,它就越难被破解,1024-bit 的 RAS 密钥基本安全,2048-bit 的 RAS 密钥很安全。而用越长的密钥来加密数据就越慢,基于 ECC(Elliptic Curve Cryptography,椭圆曲线密码学) 的算法更安全、快速,256-bit 的 ECC 密钥和 3072-bit 的 RAS 密钥的加密强度都是 128-bit,而 256-bit 的 ECDSA 密钥比 2048-bit 密钥的 RSA 进行 数字签名 快 20 倍。下表展示常用密钥长度的 加密强度 对比关系:
| Symmetric Key length | RSA key length | ECC key length |
|---|---|---|
| 80 | 1024 | 160 |
| 112 | 2048 | 224 |
| 128 | 3072 | 256 |
| 192 | 7680 | 384 |
| 256 | 15360 | 521 |
虽然 ECC 在签名生成方面更快,但在签名验证时它比 RSA 慢:
[root@CentOS ~]# openssl speed ecdsap256 rsa2048 sign verify sign/s verify/s rsa 2048 bits 0.002530s 0.000076s 395.3 13187.5 256 bit ecdsa (nistp256) 0.0001s 0.0003s 9822.3 3972.3
公钥加密最主要的用途是 密钥交换 和 身份验证/数字签名(具体实现见本文的章节 5 和章节 6),比如 DH、ECDH、ECDHE 等只用于 密钥交换,而 DSA、ECDSA 等只用于 身份验证,但是 RSA 可同时用于二者。目前最好的 密码套件(Cipher suites) 是 ECDHE 密钥交换,再结合 ECDSA 数字签名
公钥加密主要用于密钥交换和身份验证,而为了保障后续的通信安全,还需要使用对称加密来加密会话数据









1 条评论
评论者的用户名
评论时间lpchg1992
2020-03-15T16:16:18Z还是比较清晰的,赞!