Python3排序算法01 - 冒泡排序
Synopsis: 冒泡排序是一种极其简单的排序算法,它重复地走访过要排序的元素,依次比较相邻两个元素,如果他们的顺序错误就把他们调换过来,直到没有元素再需要交换,排序完成。由于它的简洁,冒泡排序通常被用来对于程序设计入门的学生介绍算法的概念。尽管冒泡排序是最容易了解和实现的排序算法之一,但它对于元素较多的序列排序时是很没有效率的
代码已上传到 https://github.com/wangy8961/python3-algorithms ,欢迎star
1. 算法介绍
冒泡排序(Bubble Sort)是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作会重复地进行,当不再有元素需要交换的时候,就表示数列排序完成了。冒泡排序与气泡上升的过程相似,气泡上升的过程中不断吸收空气而变大,冒泡排序算法也是依次比较相邻的两个元素,将较大的"浮"到最右边
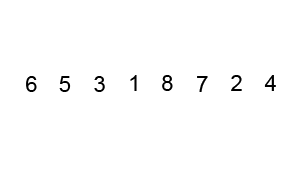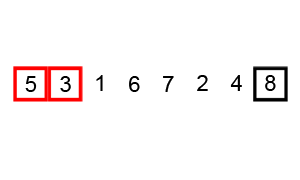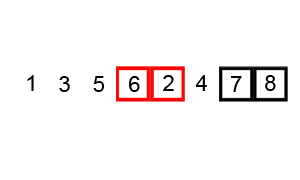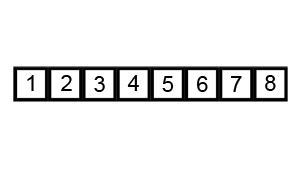
算法(假设按升序排序)的主要步骤如下:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。步骤1和步骤2合称为一次冒泡操作,每次冒泡操作会选出 "未排序序列" 的最大值,所以总共需要进行
n-1次冒泡操作 - 针对所有的元素重复以上的步骤,除了最后一个(第2次冒泡操作,序列的最后一个元素是 "已排序序列",该冒泡操作需要进行
n-2次比较) - 持续对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较(冒泡操作只针对 "未排序序列",所以每次冒泡操作的比较次数递减)
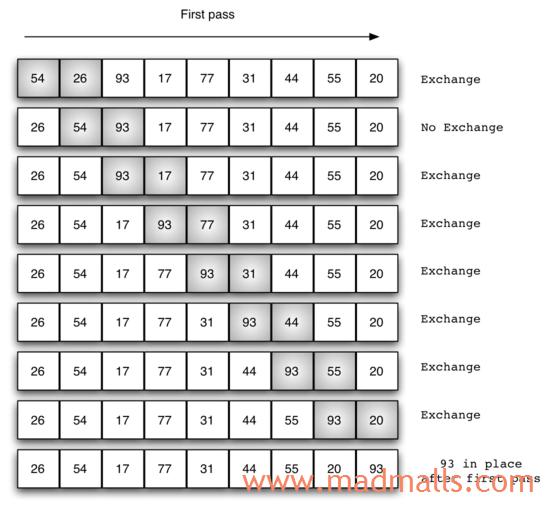
上图演示了第1次冒泡操作,该冒泡操作需要进行8次比较
2. Python实现
假设要排序拥有 n 个元素的列表L,且按升序排列
2.1 错误的算法
下面的代码只是演示错误的情形,每次冒泡操作都遍历整个序列,将当前元素与 "已排序序列" 中的元素进行比较完全是浪费时间:
def bubbLe_sort(L): '''演示错误的冒泡算法''' n = len(L) if n <= 1: return for i in range(n-1): # 共需要n-1次冒泡操作 # 每次冒泡操作都遍历整个列表的元素,即使后面已经排序好的元素也会比较,完全是在浪费时间 for j in range(n-1): # j 表示列表的下标,j不能取值n-1,否则L[j+1]会下标越界 if L[j] > L[j+1]: L[j], L[j+1] = L[j+1], L[j] if __name__ == '__main__': L1 = [54, 26, 93, 17, 77, 31, 44, 55, 20] print('Before: ', L1) bubbLe_sort(L1) print('After: ', L1) # Output: # Before: [54, 26, 93, 17, 77, 31, 44, 55, 20] # After: [17, 20, 26, 31, 44, 54, 55, 77, 93]
压力测试,使用 timeit 模块排序1000次,如果from __main__ import L,结果好像不对,所以在函数内初始化相同的L:
from timeit import timeit def bubbLe_sort(): # import random # gen = (random.randint(1, 100) for i in range(100)) # 产生100个 1-99 范围内的随机整数 # L = list(gen) L = [96, 2, 65, 23, 47, 58, 8, 48, 69, 92, 34, 83, 93, 47, 45, 55, 95, 15, 92, 24, 64, 19, 29, 55, 35, 48, 39, 29, 63, 94, 99, 38, 50, 10, 10, 93, 74, 27, 74, 44, 29, 81, 85, 86, 74, 30, 50, 50, 12, 12, 38, 75, 41, 87, 80, 97, 16, 48, 65, 69, 83, 71, 28, 9, 64, 69, 27, 74, 74, 86, 40, 69, 79, 79, 77, 100, 53, 72, 77, 16, 8, 36, 41, 58, 59, 29, 46, 79, 81, 66, 8, 35, 60, 52, 2, 82, 2, 36, 79, 66] n = len(L) for i in range(n-1): for j in range(n-1): if L[j] > L[j+1]: L[j], L[j+1] = L[j+1], L[j] return L print('Bubble sort function run 1000 times, cost: ', timeit('bubbLe_sort()', 'from __main__ import bubbLe_sort', number=1000), 'seconds.') # Output # Bubble sort function run 1000 times, cost: 2.900782099 seconds.
2.2 正确的算法
每次冒泡操作只针对 "未排序序列",所以每次冒泡操作的比较次数递减:
| 冒泡操作次数 | 比较的次数 |
|---|---|
| 第1次,i = 0 | n-1 |
| 第2次,i = 1 | n-2 |
| 第3次,i = 2 | n-3 |
| ... | ... |
| 第n-1次,i = n-2 | 1 |
助记:每次冒泡操作需要
n-i-1次比较













0 条评论
评论者的用户名
评论时间暂时还没有评论.