Python3排序算法05 - 归并排序
Synopsis: 归并排序(Merge Sort)是建立在归并操作上的一种有效的排序算法,它将已经有序的子序列合并,得到完全有序的序列。也就是说,先使每个子序列有序(单个元素组成的序列肯定是有序的),再将两个有序序列合并成一个更大的有序序列。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,将复杂的问题分解成容易解决的小问题,比如将两个只有一个元素的左右子序列排序合并很简单,再一层层合并成更大的有序序列
代码已上传到 https://github.com/wangy8961/python3-algorithms ,欢迎star
1. 算法介绍
归并排序(Merge Sort)算法于1945年由约翰·冯·诺伊曼首次提出,它是采用分治法(Divide and Conquer)的一个典型的应用,是创建在归并操作(Merge)上的一种有效的排序算法,时间复杂度为O(n log n)
2. Python实现
归并排序算法依赖归并操作。归并操作是将 两个已经排序的序列 合并成一个序列的操作:
def merge(left, right): '''归并操作,使用可移动游标''' left_index = 0 # left序列的可移动的下标 right_index = 0 # right序列的可移动的下标 merged = [] # 用来存放最终排好序的元素 while left_index < len(left) and right_index < len(right): # 一旦 left序列 或 right序列 中的元素比较完成,就退出循环 if left[left_index] < right[right_index]: merged.append(left[left_index]) left_index += 1 # left序列的下标向右移动一位 else: merged.append(right[right_index]) right_index += 1 # right序列的下标向右移动一位 merged = merged + left[left_index:] # 如果 left序列 还有没比较的元素 merged = merged + right[right_index:] # 如果 right序列 还有没比较的元素 return merged
或者:
from collections import deque def merge(left, right): '''归并操作,使用deque''' merged, left, right = [], deque(left), deque(right) while left and right: merged.append(left.popleft() if left[0] <= right[0] else right.popleft()) # deque popleft is also O(1) merged.extend(right if right else left) # 如果 left序列 还有没比较的元素 return merged
2.1 递归法 - 自顶向下(Top Down)
def merge_sort(L): n = len(L) # 两个作用: # 1. 客户端传入原始序列只有一个元素或为空时,不用排序,直接返回 # 2. 递归的退出条件。如果传入的序列元素个数为1时,不再拆分,返回 if n <= 1: return L # 将传入的序列拆分成左右两个子序列,再分别递归 mid = n // 2 left = merge_sort(L[:mid]) # 特别注意:先递归左边的,直到子序列元素为1个,才依次向上返回。比如L = [54, 26, 93, 17, 77, 31, 44, 55, 20],则会先将 [54, 26, 93, 17] 归并排序好之后才会排右边的 right = merge_sort(L[mid:]) # 开始执行归并操作,将结果返回给上一层的 merge_sort() 调用栈 return merge(left, right) def merge(left, right): '''归并操作,使用可移动游标''' left_index = 0 # left序列的可移动的下标 right_index = 0 # right序列的可移动的下标 merged = [] # 用来存放最终排好序的元素 while left_index < len(left) and right_index < len(right): # 一旦 left序列 或 right序列 中的元素比较完成,就退出循环 if left[left_index] < right[right_index]: merged.append(left[left_index]) left_index += 1 # left序列的下标向右移动一位 else: merged.append(right[right_index]) right_index += 1 # right序列的下标向右移动一位 merged = merged + left[left_index:] # 如果 left序列 还有没比较的元素 merged = merged + right[right_index:] # 如果 right序列 还有没比较的元素 return merged def is_sorted(L): '''辅助函数: 用来判断 '归并排序函数(merge_sort)' 的输出结果是否是正确的升序序列''' prev = L[0] for i in range(1, len(L)): if prev > L[i]: print('Sort ascending failed.') return False prev = L[i] print('Sort ascending succeed.') return True if __name__ == '__main__': L1 = [54, 26, 93, 17, 77, 31, 44, 55, 20] print('Before: ', L1) merged = merge_sort(L1) if is_sorted(merged): print('After: ', merged) # Output: Before: [54, 26, 93, 17, 77, 31, 44, 55, 20] Sort ascending succeed. After: [17, 20, 26, 31, 44, 54, 55, 77, 93]
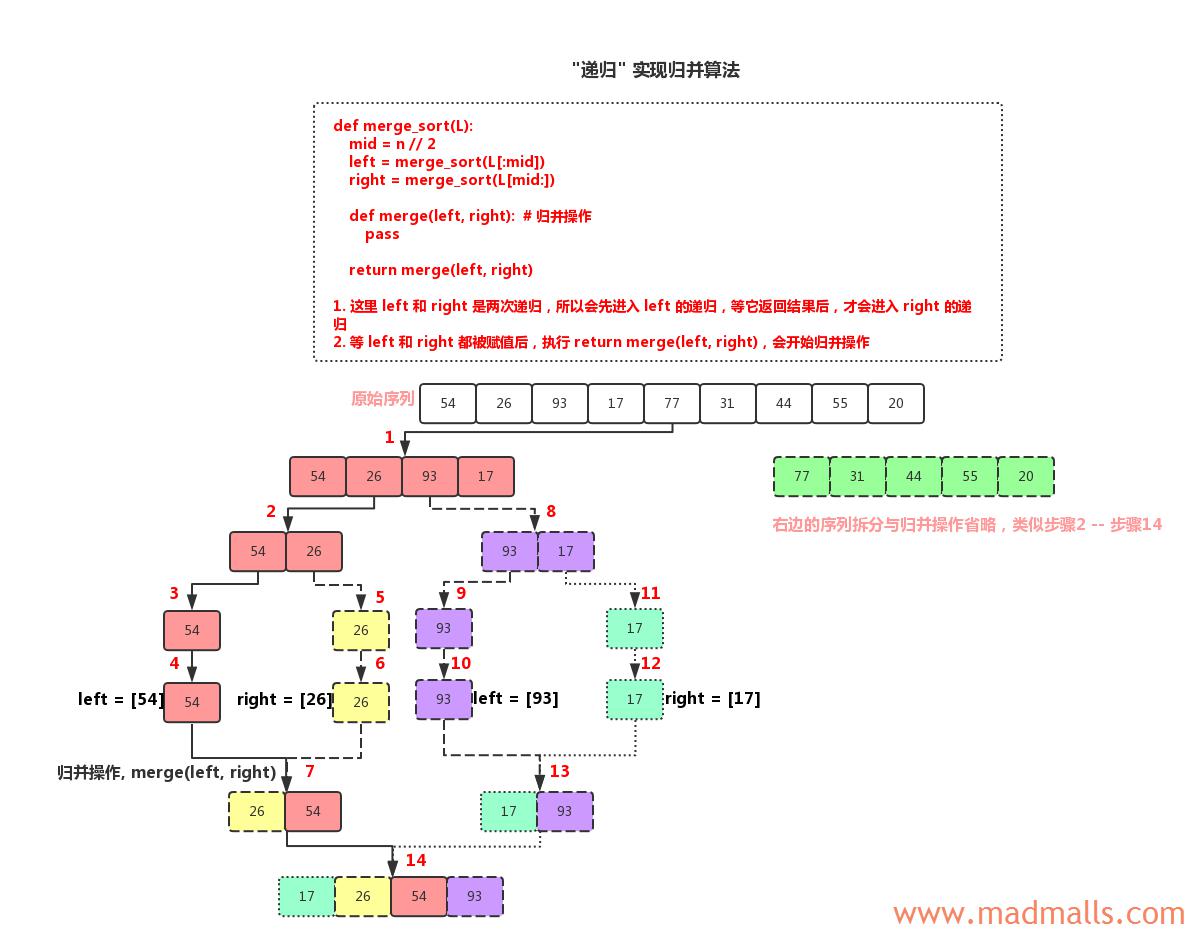
过程分析:
Step 1: 对应上图中标号1,执行 merged = merge_sort([54, 26, 93, 17, 77, 31, 44, 55, 20]) 时,n = 9,mid = 4
执行到 left = merge_sort([54, 26, 93, 17]) 后,将会第1次递归执行merge_sort函数,所以后续的 right = merge_sort([77, 31, 44, 55, 20]) 暂时不会执行
Step 2: 对应上图中标号2,(第1次递归)执行 left = merge_sort([54, 26, 93, 17]) 时,n = 4,mid = 2
执行到 left = merge_sort([54, 26]) 后,将会第2次递归执行 merge_sort 函数
Step 3: 对应上图中标号3,(第2次递归)执行 left = merge_sort([54, 26]) 时,n = 2,mid = 1
执行到 left = merge_sort([54])时,将会第3次递归执行 merge_sort 函数
Step 4: 对应上图中标号4,(第3次递归)执行 left = merge_sort([54]) 时,n = 1,返回 [54],第3次递归结束! 所以 left = [54]
Step 5: 对应上图中标号5,返回到第2次递归中,执行 right = merge_sort([26])












0 条评论
评论者的用户名
评论时间暂时还没有评论.