Synopsis: 算法是设计良好的可计算的过程，它把某个值或某些值作为输入并产生某个值或某些值作为输出。通常设计一个解决问题的算法是很容易的，但如果这个算法很慢，就要重新设计了。因为算法运行的速度取决于它运行的环境以及实现的细节，计算机科学家们倾向于把运行时间以输入的大小来表示，比如O(n)

代码已上传到 https://github.com/wangy8961/python3-algorithms ，欢迎star

1. 特征

An algorithm is a sequence of unambiguous instructions used for solving a problem, which can be implemented (as a program) on a computer

算法是解决问题的方法，可以用不同的计算机语言去实现该算法，重要的是算法的思想！

algorithm

算法的五个特征如下：

输入（Input）：一个算法必须有0个或0个以上输入量。Every algorithm must take zero or more number of input values from external.
输出（Output）：一个算法应有1个或1个以上输出量，输出量是算法计算的结果。Every algorithm must produce an output as result.
明确性（Definiteness）：算法的描述必须无歧义，算法中的每个语句/指令都必须清晰明确（只有一种解释）。Every statement/instruction in an algorithm must be clear and unambiguous (only one interpretation)
有限性（Finiteness）：算法必须在有限个步骤内完成任务。For all different cases, the algorithm must produce result within a finite number of steps.
有效性（Effectiveness）：又称可行性，算法中描述的每个操作，都可以通过执行有限次的基本运算来实现。Every instruction must be basic enough to be carried out and it also must be feasible.

2. 算法的性能

一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。Performance analysis of an algorithm is the process of calculating space required by that algorithm and time required by that algorithm.

2.1 时间复杂度

算法的时间复杂度(Time Complexity)是指算法需要消耗的时间。一般来说，计算机算法是问题规模 n 的函数 f(n)，算法执行时间的增长率与 f(n) 的增长率正相关，称作渐近时间复杂度，简称时间复杂度

时间复杂度常用大O符号（Big Oh）表述，不包括这个函数的低阶项和首项系数，算法的时间复杂度也因此记做：T(n) = O(f(n))

常见的时间复杂度有：

O(1)：常数阶（不会随 n 的大小而改变）
O(log n)：对数阶
O(n)：线性阶
O(n log n)：线性对数阶
O(n²)：平方阶
O(n³)：立方阶
O(2^n)：指数阶
O(n!)：阶乘阶

随着问题规模 n 的不断增大，上述时间复杂度不断增大，算法的执行效率越低

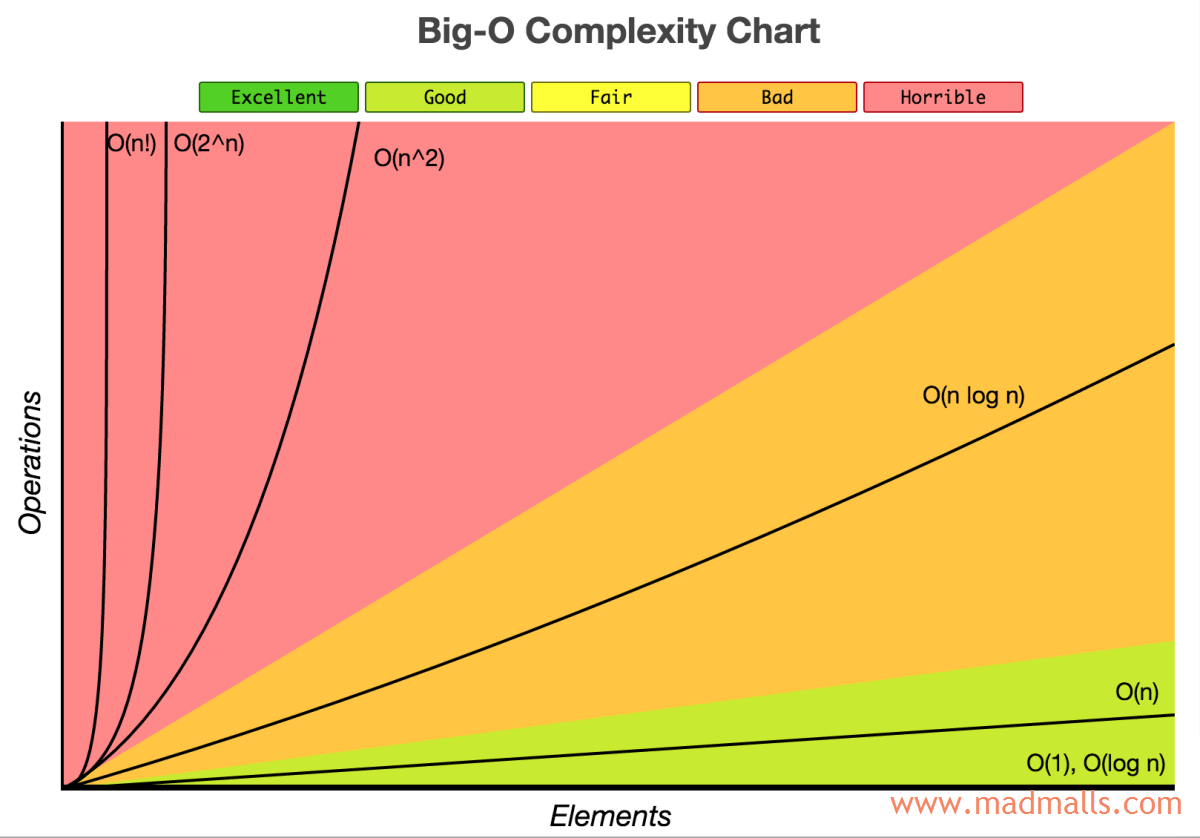
时间复杂度

注意：主要关注算法的最坏时间复杂度

2.2 空间复杂度

算法完成其执行所需的计算机内存总量称为该算法的空间复杂度(Space Complexity)，它的计算和表示方法与时间复杂度类似，一般都用复杂度的渐近性来表示，记做：S(n) = O(f(n))

通常，当程序运行时，需要计算机内存用于以下情况：

Instruction Space： It is the amount of memory used to store compiled version of instructions.
Environmental Stack： It is the amount of memory used to store information of partially executed functions at the time of function call.
Data Space： It is the amount of memory used to store all the variables and constants.

与时间复杂度相比，空间复杂度的分析要简单得多，我们只考虑数据空间(Data Space)并忽略指令空间以及环境堆栈，这意味着我们只计算存储变量、常量、结构等所需的内存

2.3 示例

问题： 如果a + b + c = 1000，且a^2 + b^2 = c^2（a,b,c 为自然数），如何求出a、b、c的所有可能组合？

首先创建一个timethis.py模块文件，用来统计每个算法函数耗费的时间：

import time
from functools import wraps


def timethis(func):  # 装饰器，输出被装饰的函数的运行时间
    @wraps(func)
    def wrapper(*args, **kwargs):
        start = time.process_time()
        r = func(*args, **kwargs)
        end = time.process_time()
        print('Function {}() in model {} cost: {} seconds'.format(func.__name__, func.__module__, end - start))
        return r
    return wrapper

(1) 算法1

from timethis import timethis


@timethis
def combination():  # 算法1，3层for循环，时间复杂度为O(n^3)
    for a in range(1001):
        for b in range(1001):
            for c in range(1001):
                if a**2 + b**2 == c**2 and a+b+c == 1000:
                    print("a, b, c: %d, %d, %d" % (a, b, c))


if __name__ == '__main__':
    combination()

# Output:
a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
Function combination() in model __main__ cost: 1137.25 seconds

这是一个性能很差的算法，我的笔记本CPU i5-3210M 2.50GHz，内存8GB，运行该算法需要1137.25秒！如果n由1000变为10000，即增长为10倍，由于该算法的时间复杂度为O(n^3)，所以运行时间大概需要1137000秒，恐怖...

(2) 算法2

from timethis import timethis


@timethis
def combination():  # 算法2，2层for循环，时间复杂度为O(n^2)
    for a in range(1001):
        for b in range(1001-a):
            c = 1000 - a - b
            if a**2 + b**2 == c**2:
                print("a, b, c: %d, %d, %d" % (a, b, c))


if __name__ == '__main__':
    combination()

# Output:
a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
Function combination() in model __main__ cost: 0.65625 seconds

改进后的算法只要0.66秒。如果n由1000变为10000，由于该算法的时间复杂度为O(n^2)，所以运行时间大约为100倍：

from timethis import timethis


@timethis
def combination():  # 算法2，2层for循环，时间复杂度为O(n^2)
    for a in range(10001):
        for b in range(10001-a):
            c = 10000 - a - b
            if a**2 + b**2 == c**2:
                print("a, b, c: %d, %d, %d" % (a, b, c))


if __name__ == '__main__':
    combination()

# Output:
a, b, c: 0, 5000, 5000
a, b, c: 2000, 3750, 4250
a, b, c: 3750, 2000, 4250
a, b, c: 5000, 0, 5000
Function combination() in model __main__ cost: 62.90625 seconds

3. 排序算法

常见的排序算法：冒泡排序、选择排序、插入排序、希尔排序、堆排序、快速排序、归并排序、计数排序、基数排序

排序算法的稳定性：

假设要对列表[(4, 1), (3, 1), (3, 7), （5, 6）]按每个元素（是一个元组）的第1个值进行升序排序，不同的排序算法可以会出现以下两种结果：

[(3, 1), (3, 7), (4, 1), （5, 6）]，其中元素(3, 1)和(3, 7)维持它们排序前的次序，则称该排序算法是稳定的
[(3, 7), (3, 1), (4, 1), （5, 6）]，其中元素(3, 1)和(3, 7)的次序与它们排序前不同，则称该排序算法是不稳定的

稳定的排序算法：

冒泡排序、插入排序、归并排序、计数排序、基数排序、桶排序

不稳定的排序算法：

选择排序、快速排序、希尔排序、堆排序