代码已上传到 https://github.com/wangy8961/python3-algorithms ，欢迎star

1. 树

树（tree）是一种抽象数据类型（ADT），用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合，把它叫做 "树" 是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

• 每个节点有零个或多个子节点
• 没有父节点的节点称为根节点
• 每一个非根节点有且只有一个父节点
• 除了根节点外，每个子节点可以分为多个不相交的子树

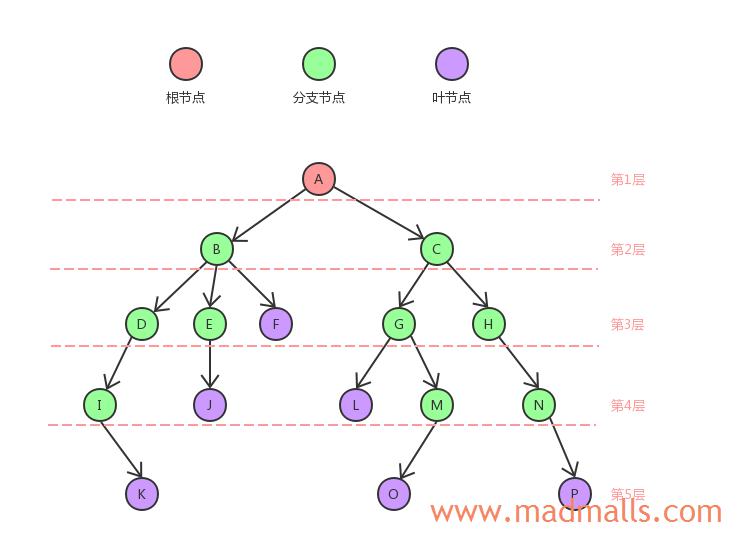
1.1 术语

参考 https://en.wikipedia.org/wiki/Tree_(data_structure)

• 子节点（Child）： 一个节点含有的子树的根节点称为该节点的子节点。比如上图中，节点B往下也是一棵树，这个子树的根节点就是B，所以节点B是节点A的子节点（该子树是节点A的左子树）；同理，节点C也是节点A的子节点
• 父节点或双亲（Parent）： 若一个节点含有子节点，则这个节点被称为其子节点的父节点。比如上图中，节点A就是节点B或节点C的父节点
• 兄弟节点（Siblings）： 具有相同父节点的节点互称为兄弟节点。比如上图中，节点B和节点C的父节点都是A，所以他俩是兄弟节点
• 节点的层次（Level）： 从根节点开始算起，根为第1层，根的子节点为第2层，以此类推
• 堂兄弟节点： 父节点在同一层的节点互为堂兄弟。比如上图中，节点F的父节点是B，节点G的父节点是C，他俩的父节点在同一层，所以节点F和G是堂兄弟
• 节点的祖先（Ancestor）： 从根到该节点所经分支上的所有节点。比如上图中，节点K的祖先是A、B、D、I
• 节点的子孙（Descendant）： 以该节点为根的子树中任一节点都称为该节点的子孙。比如上图中，节点B的子孙是D、E、F、I、J、K
• 节点的度（Degree）： 一个节点含有的子树的个数称为该节点的度。比如上图中，节点A的度是2，节点B的度是3，节点K的度是0
• 叶节点（Leaf node）： 度为零的节点。比如上图中，节点K、J、F、L、O、P都是叶节点
• 分支节点（Branch node）： 度不为零的节点
• 树的度： 一棵树中，最大的节点的度称为树的度。比如上图中，节点B的度为3，它是所有节点中度最大的，所以树的度是3
• 节点的深度（Depth of node）： 对于任意节点，它的深度为从根节点到它的唯一路径长。比如上图中，节点B的深度为1，节点K的深度为4，节点A的深度为0（根节点的深度为0）
• 节点的高度（Height of node）： 对于任意节点，它的高度为从它到叶节点的最长路径长。比如上图中，节点B到叶节点K的路径长为3，到叶节点J的路径长为2，到叶节点F的路径长为1，所以节点B的高度为3； 叶节点的高度都为0
• 树的高度（Height of tree）： 树的高度是其根节点的高度
• 森林（Forest）： 由m（m>=0）棵互不相交的树的组成的集合，称为森林

1.2 树的种类

• 无序树： 树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树
• 有序树： 树中任意节点的子节点之间有顺序关系，这种树称为有序树
  • 二叉树： 每个节点最多含有两个子树的树称为二叉树
    • 完全二叉树： 对于一颗二叉树，假设其深度为d（d>1）。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树
      • 满二叉树： 所有叶节点都在最底层的完全二叉树
    • 平衡二叉树（AVL树）： 当且仅当任何节点的两棵子树的高度差不大于1的二叉树