Synopsis: 希尔排序按其设计者希尔（Donald Shell）的名字命名，该算法由1959年公布。希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）

代码已上传到 https://github.com/wangy8961/python3-algorithms ，欢迎star

1. 算法介绍

希尔排序（Shell Sort）也称递减增量排序算法（diminishing increment sort），是插入排序的一种更高效的改进版本。假设有一个很小的值在序列的最右边，按 "升序" 排列的话要将它移动到最左边，插入排序每次只能从右向左移动一位，可能会进行 n 次比较和交换才能将该数据移至正确位置。而希尔排序会用较大的步长移动数据，所以只需要进行少数次比较和交换就可到正确位置

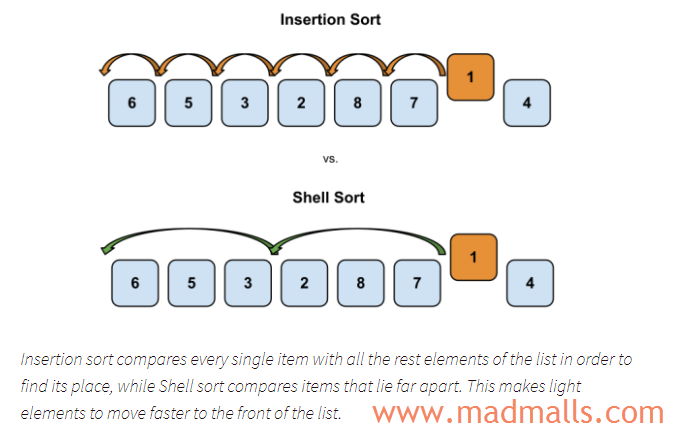
Shell Sort 00

算法的主要步骤如下：

选择一个最初步长，将原始序列分为几个区域，针对每个区域分别进行插入排序
第1步完成后，将步长取半，再将第1步排序后的序列又分为几个区域，分别进行插入排序
依次类推，直到步长为1时，此时序列几乎已经按升序排好序了，再进行插入排序（插入排序针对几乎已经排好序的序列，效率高）

第1次选择步长 gap = 4 ：

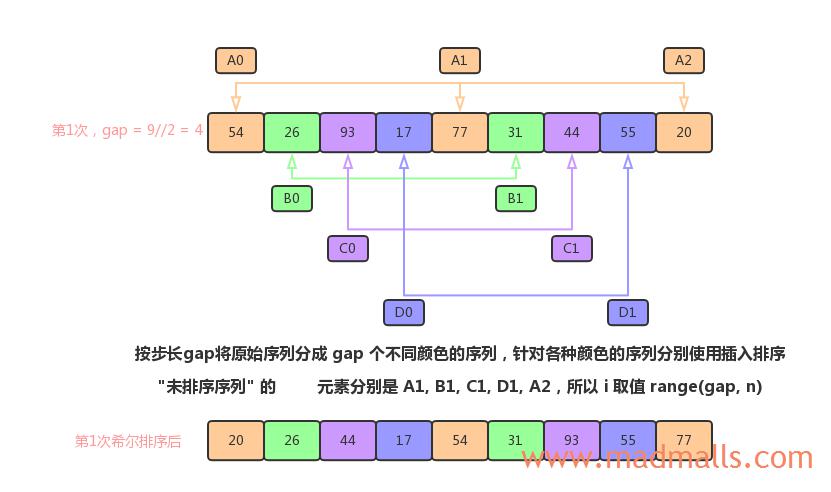
Shell Sort 01

第2次选择步长 gap = 2 ：

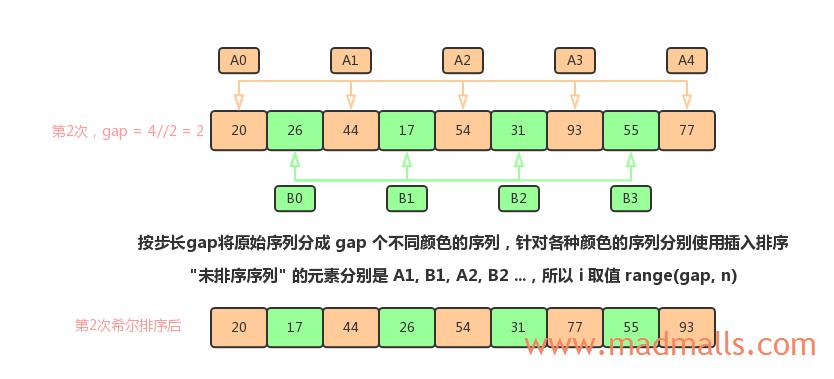
Shell Sort 02

第3次选择步长 gap = 1 ，即普通的插入排序，只不过此时序列几乎已经排好序了，所以插入排序效率高：

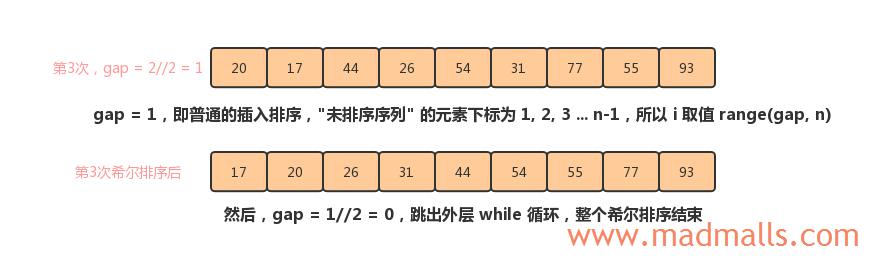
Shell Sort 03

2. Python实现

步长的选择是希尔排序的重要部分

2.1 算法1

Donald Shell建议最初步长选择为 n / 2，后续不断对步长取半，直到步长达到1

def shell_sort(L):
    '''希尔排序，升序'''
    n = len(L)
    if n <= 1:
        return

    gap = n // 2  # 初始步长
    while gap > 0:  # 最后一次步长为1（即普通的插入排序），然后整个希尔排序结束

        # 想像成，以步长 gap 将原始序列划分成 gap 个待排序的序列，对每个序列使用普通的插入排序进行排序
        # 序列1: [L[0], L[gap], L[2*gap]...]
        # 序列2: [L[1], L[1+gap], L[1 + 2*gap]...]
        # 序列3: [L[2], L[2+gap], L[2 + 2*gap]...]
        # 请查看插入排序算法 https://github.com/wangy8961/python3-algorithms/blob/master/4.%20%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F%20-%20Insertion%20Sort/3_best_insertion_sort_asc.py
        # 助记：普通的插入排序算法中步长是 1 ，把插入排序中的步长 1 替换为 gap
        for i in range(gap, n):  # "未排序序列" 的第1个元素分别是L[gap], L[1+gap], L[2+gap] ... ，所以变量 i 表示的下标是 gap, 1+gap, 2+gap ...
            temp = L[i]
            j = i
            # j >= gap是因为后续j[j-gap]，否则下标越界
            while j >= gap and temp < L[j-gap]:
                L[j] = L[j-gap]
                j -= gap
            L[j] = temp

        gap = gap // 2  # 得到新的步长


if __name__ == '__main__':
    L1 = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print('Before: ', L1)
    shell_sort(L1)
    print('After: ', L1)

    # Output:
    # Before:  [54, 26, 93, 17, 77, 31, 44, 55, 20]
    # After:  [17, 20, 26, 31, 44, 54, 55, 77, 93]

压力测试：

from timeit import timeit


def shell_sort():
    # import random
    # gen = (random.randint(1, 100) for i in range(100))  # 产生100个 1-99 范围内的随机整数
    # L = list(gen)
    L = [96, 2, 65, 23, 47, 58, 8, 48, 69, 92, 34, 83, 93, 47, 45, 55, 95, 15, 92, 24, 64, 19, 29, 55, 35, 48, 39, 29, 63, 94, 99, 38, 50, 10, 10, 93, 74, 27, 74, 44, 29, 81, 85, 86, 74, 30, 50, 50, 12, 12, 38, 75, 41, 87, 80,