Synopsis: 插入排序是一种简单直观的排序算法，它的工作原理非常类似于我们抓扑克牌，对于未排序数据(右手抓到的牌)，在已排序序列(左手已经排好序的手牌)中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用 in-place sorting，即只需用到 O(1) 的额外空间的排序，因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间

代码已上传到 https://github.com/wangy8961/python3-algorithms ，欢迎star

1. 算法介绍

插入排序（Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序序列中的某个数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间

抓扑克牌

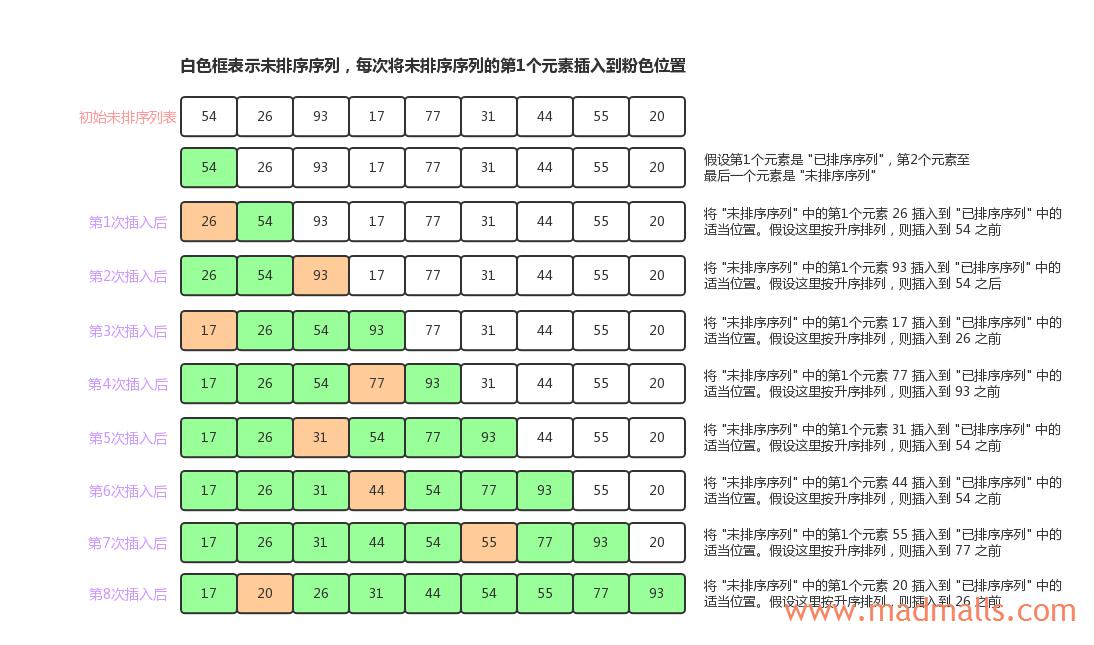
算法（假设按升序排序）的主要步骤如下：

将初始未排序序列的第1个元素当作一个已排序序列，把第2个元素到最后一个元素当作未排序序列
从头到尾依次扫描未排序序列，将扫描到的每个元素插入已排序序列的适当位置（从后向前扫描已排序序列）。如果待插入的元素与已排序序列中的某个元素相等，则将待插入的元素插入到相等元素的后面

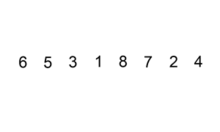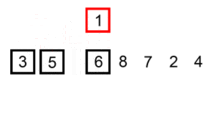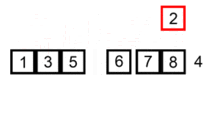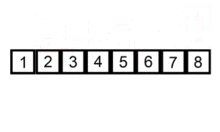
Insertion Sort 01

2. Python实现

Insertion Sort 02

2.1 算法1

相当于将 L[i] 与 "已排序序列" 中的元素（从后向前）依次比较，如果 L[i] 比较小，则交换位置。使用 while 循环和元组解包（Tuple Unpacking） 就地交换两个元素的值：

def insertion_sort(L):
    '''插入排序，升序
    相当于将L[i]与 "已排序序列" 中的元素(从后向前)依次比较，如果L[i]比较小，则交换位置
    '''
    n = len(L)
    if n <= 1:
        return

    # 首先，假设第1个元素L[0]是 "已排序序列"，第2个元素L[1]至最后一个元素L[n-1]是 "未排序序列"
    for i in range(1, n):  # 未排序的元素有 n-1 个，所以共需要 n-1 次插入操作。 i 表示 "未排序序列" 的第1个元素的下标，所以 i 从下标 1 开始

        # 将 "未排序序列" 的第1个元素和 "已排序序列" 从后向前，每两个元素之间比较，如果顺序不对就交换它俩的位置
        # 使用while循环
        j = i
        # j >= 1是因为后续j[j-1]，否则下标越界
        while j >= 1 and L[j] < L[j-1]:  # 第1次是比较 "未排序序列" 的第1个元素和 "已排序序列" 的最后1个元素
            L[j], L[j-1] = L[j-1], L[j]
            j -= 1


if __name__ == '__main__':
    L1 = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    print('Before: ', L1)
    insertion_sort(L1)
    print('After: ', L1)

    # Output:
    # Before:  [54, 26, 93, 17, 77, 31, 44, 55, 20]
    # After:  [17, 20, 26, 31, 44, 54, 55, 77, 93]

压力测试：

from timeit import timeit


def insertion_sort():
    # import random
    # gen = (random.randint(1, 100) for i in range(100))  # 产生100个 1-99 范围内的随机整数
    # L = list(gen)
    L = [96, 2, 65, 23, 47, 58, 8, 48, 69, 92, 34, 83, 93, 47, 45, 55, 95, 15, 92, 24, 64, 19, 29, 55, 35, 48, 39, 29, 63, 94, 99, 38, 50, 10, 10, 93, 74, 27, 74, 44, 29, 81, 85, 86, 74, 30, 50, 50, 12, 12, 38, 75, 41, 87, 80, 97, 16, 48, 65, 69, 83, 71, 28, 9, 64, 69, 27, 74, 74, 86, 40, 69, 79, 79, 77, 100, 53, 72, 77, 16, 8, 36, 41, 58, 59, 29, 46, 79, 81, 66, 8, 35, 60, 52, 2, 82, 2, 36, 79, 66]

    n = len(L)
    for i in range(1, n):
        j = i
        while j >= 1 and L[j] < L[j-1]:
            L[j], L[j-1]